Rodrigues Formula

已知旋转向量为$\theta k$，其中$k$为旋转轴上的单位向量，$|k|=1$，$\theta$为绕旋转轴旋转过的角度，证明Rodrigues formula:

$$R=\cos\theta I+(1-\cos\theta)kk^T+\sin\theta k^\times$$

其中，R为对应的旋转矩阵。

设$v$为将被旋转的向量，将其分解为与$k$平行方向及与$k$垂直方向上的两个分量$v_{||}$,$v_{\bot}$。分解如下图所示：

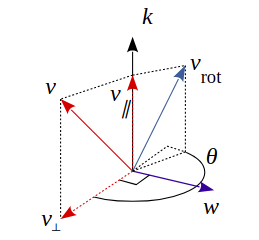
可得：

$$v=v_{||}+v_\bot$$

其中，由投影可知：

$$v_{||}=(v\cdot k)k$$ $$v_\bot=-k\times(k\times v)$$

将$v$绕$k$轴旋转$\theta$角，即分别将其的两个分量绕$k$轴旋转$\theta$角，旋转后的矢量为：

$$v_{rot}=v_{||rot}+v_{\bot rot}$$ $$v_{\bot rot}=\cos\theta v_\bot+\sin\theta(k\times v_\bot)$$

由于与$k$轴平行的分量旋转并不发生变化，所以：

$$v_{||rot}=v_{||}$$

其中

$$k\times v_\bot=k\times (v-v_{||})=k\times v-k\times v_{||}=k\times v$$

所以：

$$v_{rot}=v_{||}+\cos\theta v_\bot+\sin\theta(k\times v)\\ =v-v_\bot+\cos\theta v_\bot+\sin\theta(k\times v)\\ =v+(1-\cos\theta)k\times(k\times v)+\sin\theta(k\times v)\\ =v+(1-\cos\theta)k^\times k^\times v+\sin\theta k^\times v$$

其中$k^\times$为k的反对称矩阵，即

$$k^\times=\left[ \begin{matrix} 0 & -k_3 & k_2\\ k_3 & 0 & -k_1\\ -k_2 & k_1 &0 \end{matrix} \right]$$

叉积用矩阵表达为:

$$k\times v=k^\times v$$

通过计算可知：

$$I+k^\times k^\times=kk^T$$

代入得：

$$v_{rot}=v+(1-\cos\theta)(kk^T-I)v+\sin\theta k^\times v\\ =\cos\theta Iv+(1-\cos\theta)kk^Tv+\sin\theta k^\times v\\ =(\cos\theta I+(1-\cos\theta)kk^T+\sin\theta k^\times)v$$

又：

$$v_{rot}=Rv$$

所以：

$$R=\cos\theta I+(1-\cos\theta)kk^T+\sin\theta k^\times$$

证毕。